今回紹介する「統計学の極意」（草思社）という本の一番大きな特徴は、数式がまったく出て来ないことです。前半は、統計学の応用について学ぶパートになっています。現実の課題解決に活用されている「事例」に触れながら、統計学について学ぶことから始まります。

最初に紹介されるのは、イギリスの医師ハロルド・シップマンが起こした殺人事件です。ある患者の死後に遺書を調べたところ、改ざんされていることが発覚しました。シップマンの手に多くの遺産が入るよう、不正に書き換えられていたのです。

火葬されていなかった他の患者を調べてみたところ、致死量の鎮痛剤を使って行われた15件の殺人事件が見付かりました。

イギリス史上最悪のシリアルキラー

その後、シップマンの患者の死亡時間についてよく調べてみると、多くの患者が夕方頃に亡くなっているという「偏り」が見付かりました。統計学を応用して調査した結果、数多くの余罪が発見され、イギリス最大の連続殺人へと発展します。

シップマンはなぜ、大量の殺人を行うことができたのでしょうか。産業医として勤めていた頃、高齢者を扱うことが多かったため、というのが一つの理由です。担当患者の死亡率の高さに同僚が疑惑を抱き始めた頃に、シップマンは巧妙にも開業医に転身します。その後、若い患者に毒牙を伸ばし始め、最大で493件、少なくとも215件の殺人を犯したとされています。

殺された患者が1回でも検死されていたら、殺人であることが判明したはずです。死亡時刻のデータが統計処理されていたら、時間の偏りが見付かったはずです。必要なデータは常にそこにあったはずなのに、事件の発見にはつながりませんでした。

新しい統計学の学び方

「PPDAC問題解決サイクル」というものがあります。最初の「P」は「Probrem」で、問題を定義する部分です。続いて「Plan（計画）」、「Data（データ）」、「Analysis（分析）」と続きます。最後の「C」には二つの意味があり、「Conclusion（結論）」と「Communication（伝達）」です。

シップマンのケースを見て分かるのは、「データ（D）」を「分析（A）」すれば答えが見い出せる訳ではない、という現実です。まず「問題意識（P）」が先に立ち、そしてどのように問題を解決するかという「計画（P）」を立てる必要があります。データを分析した後は、結果を分かりやすく提示する「可視化（Cに相当）」が必要になります。

「データ（D）」と「分析（A）」は、問題解決のプロセスの中でほんの一部分でしかありません。それなのに多くの人は、データや分析手法ばかりを学びたがります。

「統計学を学ぶ」ために必要なことは、単に「データの加工方法や分析のために使う公式を覚える」ということだけではありません。課題をどのようにして数として捉え、どのように分析するのかという「視点」がとても重要なのです。

課題解決に使われている具体的なケースを通じて、統計学の基本を学ぶのが「統計学の極意」の前半部分が目指すところです。平均や標準偏差というような基本から始まり、回帰モデルや機械学習に使われる基本的な手法までをカバーします。ちなみに、シップマンのケースは、現代なら普通に使われているコンピュータによる分析手法によって容易に判明したはずだ、と言われています。

ギャンブルの確率計算

書籍の後半部分では、確率・統計についてより専門的な解説が繰り広げられます。冒頭にはギャンブルの問題が紹介されています。

次のようなゲームをするとき、A、Bどちらに賭ける方が得なのか、考えてみましょう。

どの目も均等に出るサイコロを4回振るとします。少なくとも1回「6」が出る方（A）に賭けるか、出ない方（B）に賭けるか。

これを、確率の問題と捉えて解いてみます。

サイコロを1回振って6が出る確率は「1/6」です。これを4回試行するわけなので、4をかけて「4/6」、約分すると「2/3（0.666…）」となり、Aに賭ける方がかなり得なように見えます。しかし、これは初学者が陥りがちな間違いです。

確認をするために、Pythonでちょっとしたプログラムを作ってみました。1から6までの乱数をサイコロにみたてて4回振り、1回でも6が出たら勝ち、という判定をするプログラムを作ります。このプログラムを、1万回繰り返して勝率をグラフにしてみると、勝率は緑色の線「0.666…」には収束せず、赤の「0.5」のあたりをうろうろします。

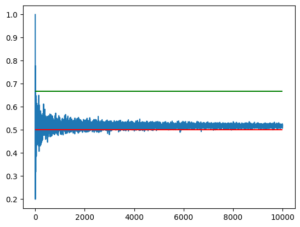
プログラムの結果を見る限り、この数値が正しい勝率で、先ほどの「2/3」という「確率の計算」は間違っていることが分かります。

これは有名な「ド・メレの問題」と呼ばれる確率の問題です。検索をすると「6が出ない確率を求めて1から引くのが正しい」、というような解説が出てきます。「6が出ない確率」とは「5/6の4乗」です。これを計算すると「625/1296」となり、「1/2（0.5）」よりわずかに小さくなります。1からこの数を引いたのがAが勝つ確率なのですから、0.5より少し多い「0.517746…」という確率になります。Pythonで出したグラフと辻褄が合いますね。

ではなぜ、「6の出る確率を4倍」すると間違いで、「6が出ない確率を求めて1から引く」と正しいのでしょうか。

全事象Ω

Wikipediaによると、数学的な確率とは「全事象Ωのうちの事象Aの割合」とあります。全事象とは「起こりうる全てのケース」のことです。1回サイコロを振るときは、「全事象Ω」は「6種類の目が出る」に、「事象A」は「6が出る」に相当します。この場合は「サイコロを1回振って6が出る確率は1/6」でまったく問題ありません。

「サイコロを4回振る」ときの全事象Ωはどうなるでしょうか。一回目は6で同じです。二回目のサイコロの世界は、一回目の6つの世界の先に、さらに6つの世界がぶら下がっている、という「見え方」をします。

こういう世界を理解するために、枝分かれをする木に見立てた「樹形図」が使われます。6本に分かれた枝が、さらに6本、また6本と、回数を追うごとに分かれて行きます。4回連続でサイコロを振るときは、6本の枝分かれが4段になるので、「6の4乗（=1296）」を計算すると全事象Ωを得ることができます。

では事象Aについてはどうでしょう。ポイントは「1回でも6が出る」という条件です。4回の試行のうち、6が2回や4回出た場合も「1回でも」6が出たことになるのです。このような条件に当てはまるケースを全て見付け出すのは結構面倒で、逆に「1回も6が出ない」確率を求めた方が楽なのです。そしてここでも樹形図を思い浮かべ、「5/6を4乗」して、全事象が起こる確率「1296/1296」から引く、という計算をするわけです。

課題の「見え方」と学び方

確率という数学を現実に適用して課題解決に利用しようとするとき、確率特有の課題の「見え方」がとても重要になります。これを押さえないと、しばしば恣意的で間違った「見え方」に引きずられてしまい、正しい答えに辿り着きません。

先ほどのPPDACのAは「確率の法則や公式」に相当する部分です。この部分だけをいくら覚えてもだめなのです。「事象を細かく分けて、しらみつぶしに数え上げる」というような課題の「見え方」の基本が分かっていないと、確率を使って現実の課題解決に利用できるようになりません。

残念ながら、よくある確率や統計の教科書は、たいてい確率の定義や公式をまず教える、というスタイルになっていることが多いのです。勉強の上手い人は「見え方」の重要性を知っているので、公式と併せてモデリングの手法を学ぼうとします。でも、多くの人は公式だけを暗記しようとします。そして、現実の課題解決に確率を適用できずに終わるのです。

「確率の極意」という書籍は、確率・統計を学ぶ時に起こるこの種の問題を見事に解決しているように思います。活用事例が世の中に溢れている「AI時代」の統計学の学び方、と言えるかも知れません。

ランダムな世界

私たちは、いろいろな種類の「予測」をしながら日常生活を送っています。私たちの頭の中には世界を表現するための「モデル」が入っていて、それを元に予測をしながら生活しています。

モデルとは簡単に言うと「法則」のようなものです。「鼻緒が切れると悪いことがある」というようなジンクスも一種のモデルと言えるかも知れません。「夕焼けが見えると翌日は晴れる」「猛暑の後は寒い冬が来る」など、天気に関するモデルはいろいろありますね。

数学を使って作られるモデルを「数学モデル」といいます。特に、確率に根ざして作られたものを「確率モデル」と呼びます。確率モデルは、数学モデルの中でも比較的新しいモデルです。そして、様々な分野で活用されているモデルでもあります。

「ほぼすべての事象はランダムに起こる」という「見え方」が根底にあるのが、確率モデルの大きな特徴です。

私たちは、身の回りの出来事に「法則性」を見い出そうとしがちです。だからこそ、「世界はランダムである」ということを受け入れられない人が多いように思います。

世界を見る「目」としての確率・統計

「世界のランダムさ」を受け入れることには、とても大きな利点があります。世界で起こる多くの事象を「確率を使って」モデル化できるのです。

身近なところでは、天気予報、出口調査を活用した選挙の当確予想、株価の予測などにも確率モデルが使われます。機械学習やデータサイエンス、AIなどの分野でも確率モデルは多用されています。

ランダムな世界の中に、かすかに際立つ特異点として発見された「ヒッグス粒子」の物語は、書籍の大きな見せ場の一つです。脳の活動を確率でとらえる「自由エネルギー理論」についても簡単に紹介されています。「脳の大統一理論」とも言われる新しい脳理論が明らかにするのは、環境の情報をデータとして取得しアルゴリズム的な「反応」を見せるコンピュータ的な脳ではなく、自らのモデルに見え方や世界を「合わせようとする」脳の姿です。

惑星の運行や高校物理に出てくる剛体などは、ニュートン力学のような「決定論」を使ってモデル化できます。私たちの世界を構成する原子や電子のように微小な粒子のモデル化は、確率を使うことで可能になります。

確率を使って原子をモデル化できなかったら、電気を伝えないはずの「半導体」を使って電子回路が作られることはなかったかも知れません。半導体がなかったら小型で高性能のコンピュータは実用化されなかったでしょう。逆に、計算量の大きい確率モデルの隆盛はコンピュータ抜きには起こりえませんでした。理論や技術は螺旋のように絡み合いながら、互いに高みを目指して登って行くものなかも知れません。

確率や統計を通して見る世界は、しばしば私たちの持つ「日常的な感覚」から大きく逸脱しています。だからこそ、「理解」した後に目の前に広がる世界は、いままでとまったく違って見えるのです。それが、確率・統計を学ぶ楽しさなのではないかと思います。