中学生の時の話です。
　小学生までは三角定規とコンパスで正三角形や正方形、六角形を書く方法などを学びます。

　中学生になると、こんどは分度器を使って正n角形を書くことを学びました。このとき書けるのは、正三角形、正四角形(正方形)、正五角形、正六角形、正八角形です。

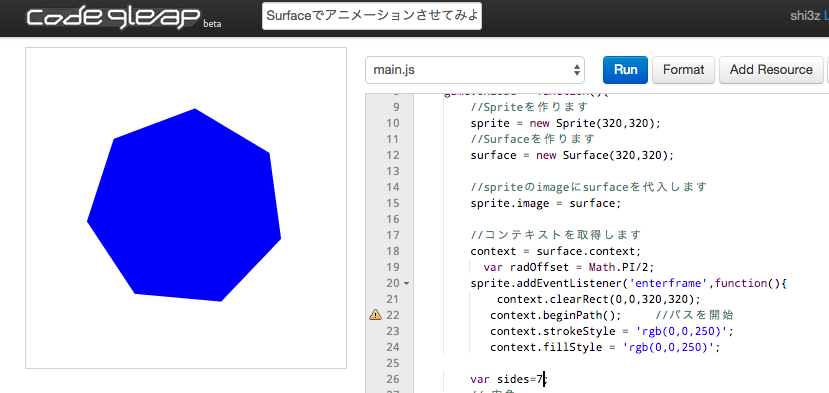
　このとき、酒井先生という数学の先生が、「正六角形以上の好きなカタチを書いておいで」という宿題を出しました。酒井先生はこうも付け加えました。「ただし、コンピュータを使う場合は20角形以上」

　思えば、これが筆者がコンピュータで宿題をする最初のきっかけとなった宿題でした。

　学校の勉強にコンピュータが使える、という驚きと喜びは、筆者を興奮させるには十分でした。

　早速家に帰り、学校で習ったことをプログラミングにしました。
　一周を360度として、3角形なら内角は120度ずつ、四角形なら90度ずつ、五角形なら72度ずつ、六角形なら60度ずつ・・・ここでふと疑問が湧き上がります。

　「はて、七角形というのを学校で習わないのはどうしてだろう?」

　答えは必然的なものでした。
　360を7で割ると、51.428571428571429…と続く無限小数になってしまうのです。すなわち、中学生で習う通常の知識と手段・・・この場合は分度器とコンパスですが・・・では、七角形は表現することができないのです。

　10までの数字で360を割り切れないのは、7だけ。20までだと、11,13,14,17,19も加わります。簡単なはずの問題が、あっという間に難題になるのです。

　ところがプログラムで書くと、内角が無理数だろうがお構いなく七角形が出現します。11角形だろうが13角形だろうが100角形だろうが余裕です。

　そこで筆者は感じたのです。「数学ってコンピュータと違わない?」と。

　プログラミングを学ぶには数学が必要であるという誤解が広まっているように感じます。もしくは、プログラミングを覚えることで数学的能力が高まるという誤解もあります。

　しかし数学とコンピュータは基本的には関係のないものです。
　みなさんがワープロを使い、Webを閲覧するのと数学が関係ないのと同じくらい、プログラミングと数学もまた関係ありません。

　そしてExcelで数学用語が出てくる程度の関係性はプログラミングと数学の間にもあります。

　数学では、正確な七角形を書くことは不可能だと教えます。
　でもそれは現実的には詭弁です。

　なぜなら、もし「正確な正七角形を書くことが出来ない」という命題が正しいとすれば、それは正三角形にも正方形にも言えることだからです。

　鉛筆を使って定規で線を引いた時、その線は鉛筆の分子のぶんの「幅」があるはずですし、数学が想定するような「太さのない直線」というものはそもそも書くことが出来ません。あくまでも、「正三角形と思しきもの」を書いて、数学的な捉え方でいえば近似して、それが「正三角形のカタチである」と思い込むことで成立しているにすぎません。

　だとすると、定規と分度器ではなく、コンピュータとプログラミング言語という道具を使って描かれた正三角形や正七角形についても認めなければなりません。無理数を使っていたとしても、画面の中に現れた正七角形はかなりリアルな正七角形のカタチを示しているはずです。

　相手が誰だったか忘れてしまいましたが、中学時代、女子に「おれは正七角形を書けるよ」とうそぶいたことがあります。その女子の反応は素直に「えー凄い。見せて見せて」というようなものだったので、僕は印刷した正七角形を見せたことがあります。

　パッと見てしまえばどうということのないカタチ、六角形と八角形の間にあるどうでもいいカタチに過ぎませんが、自分自身、なにか得体の知れないものを見てしまった、という驚きがあったことを思い出します。

　そもそもこの話は不気味かつ不可解です。
　実際にコンピュータで正七角形にかぎらず、正n角形を表示しようと思ったら、まず三角関数を使わなければなりません。三角関数への角度の入力はラジアン角です。つまり一周が360度ではなく、2πとして考える角度で、ここでいきなりπという無理数が出てきてしまいます。

　三角形だろうが正方形だろうが、このπという無理数と付き合わないとそもそも三角関数自体を扱うことが出来ないというのがどうにも奇妙な気がするのですが、現実問題としてそれ以外の手段は関数テーブルを書くくらいしかないので仕方ありません。

　120度はラジアン角では2.0943951023931953...です。気持ち悪い!さらに、sin(120度)は、0.8660254037844388...であり、cos(120度)は-0.499999999999999....です。ギャア!!!ここまでくるとほとんど恐怖を感じるレベルです。

　こんなに微妙な数字でも、画面に表示されると異常なほどの説得力があります。

　どこからどうみても正三角形です。

　これが正三角形に見えない人はいないと思いますが、この正三角形は今まさに上で示したような奇妙な計算の上で表示されているものです。

　つまり、分度器と定規の世界では極めて合理的に思える内角を使った正n角形も、コンピュータに掛かると無理数のオンパレードで、とても数学的な美しさを持っているとは言い難いが、出来上がった結果だけとを見るとなかなか美しい、というのが真相なのです。まともな数学者なら、これが数学的美しさを備えた図形だと主張したら怒り出すでしょう。それは数学的幾何学的美しさの対極にあるものだからです。なにせプログラミングした僕自身が気持ち悪いと思っているものなのですから。

　しかし皮肉なことに、今皆さんが見ているほとんど全ての図形は、このような異常かついい加減な計算の末に作られています。なにせ一般的なコンピュータがサポートしているのは、数学的精密さを持った数式の処理ではなく、浮動小数点数という、数学的に見ればデタラメな道具しかないからです。

　数学で最も美しいのは整数かもしれませんが、整数の表現ですらコンピュータは苦手です。今のコンピュータの主流は64ビットですが、64ビットで表現できる整数は0〜184,46,744,073,709,551,616というかなり中途半端なものです。負数までサポートしようとすると、-9,223,372,036,854,775,808〜9,223,372,036,854,775,808までです。

　そう考えると、なぜ一般的に360度が一周であると考えるようになったのかという数学に潜む裏側の事情が垣間見れます。要は10以下の数で割り切れる可能性が高い数の中では手頃で使いやすかったからではないでしょうか。ちなみに2,3,5,7,9の最小公倍数は630で、一周を630度とする分度器があれば七角形を書くことは可能です。ただ、一周が360度の分度器でさえ読み取るのが難しいのに、その倍近い目盛りが必要となると、分度器自体が大きくなる可能性があります。ちなみに一周が630度だと、13角形と14角形を書くことが出来るようになります。

　しかし致命的な欠点は、630を4で割るときです。
　630を4で割ると157.5となり、割り切れなくはないですが360度を4で割ると90度になることに比べると明らかに不便です。ちなみに3,4,5,7,9の最小公倍数は1260であり、1/4にすると315です。やはり90度に比べると計算上不便です。

　だとしたら、10までの数のうち、7角形だけを諦めればいろいろと都合が良くなる一周=360度が一番良い、という思想なのでしょう。

　これまでの議論でわかったとおり、数学上のルールというのは基本的に人間が決めています。
　なぜ分度器と定規で七角形や11角形が描けないのか、これでわかりました。要はみんなが便利だと決めたルールから逸脱しているからです。

　同じ理由で、三角関数の引数がラジアン角であることもわかります。近代のコンピュータでは、三角関数をテイラー展開で求めます。このテイラー展開の前提が、三角関数に渡される角度はラジアン角であるという前提があるからです。

　なぜラジアン角なのかといえば、テイラー展開による三角関数を求めるためには、オイラーの公式が前提としてあるからです。

　このオイラーの公式で、θ=πのときに-1になることが示されています。これをオイラーの等式といいます。三角関数のテイラー展開はこの等式から導かれます。

　これを複素平面上の円が半周している時に成立していると考えることにしています。そのため、半周をπとする(つまり一周を2πとする)ラジアン角が必要になるというわけです。一見、理不尽で気持ちが悪くても、調べればなんらかの理由はあるわけです。

　僕はたまたま、七角形がなぜ分度器で描けないのか、という興味から、数学の成り立ちについて学ぶきっかけになりましたが、数学の先生に「どうして七角形をコンピュータが描くのは簡単なのに、分度器では描けないんだ」と聞いてもちゃんと答えてもらえなかったことを覚えています。

　まあ子供にテイラー展開について説明するのが面倒だったのでしょう。もしくは深く考えていなかったか。どちらかです。

　数学は人工言語の一種なので、いろんなところに人間が決めた都合が見え隠れします。「なぜなのか」考えるのは頭の体操としては面白いのですが、コンピュータは現実の問題を解くための道具に過ぎません。

　コンピュータでは、数学の高度な概念はどんどん隠蔽されていきます。むしろ隠蔽するためにソフトウェア工学が発達したのではないかと思えるフシもあります。

　誰もわざわざややこしいことに頭を使いたくないのです。

　プログラミングと数学は根本的に違うものですが、だからこそお互いがお互いを補完しあって面白いのではないか、と僕は思います。